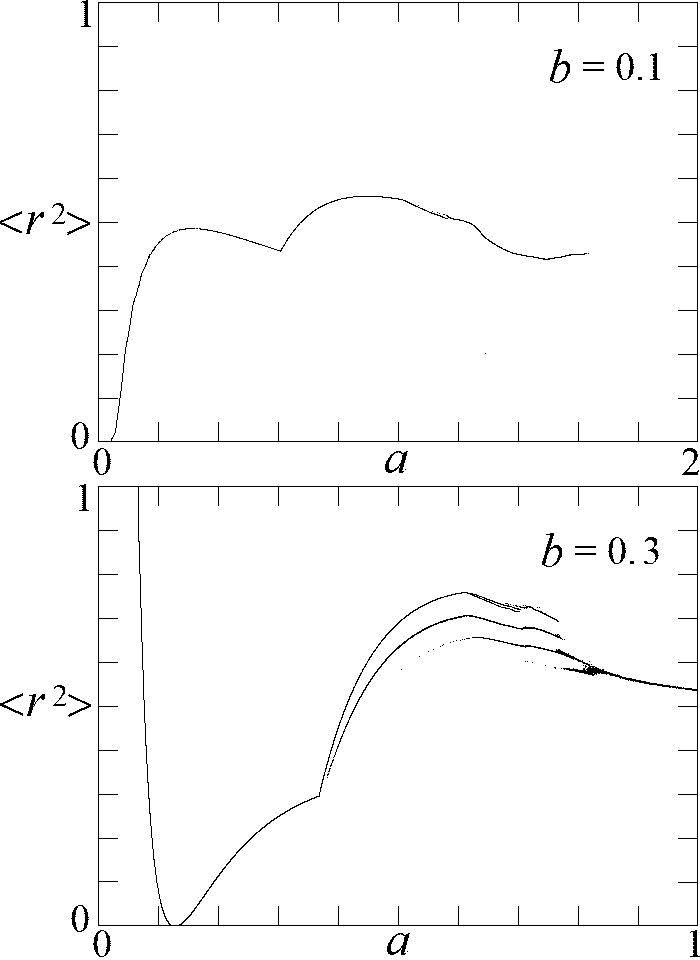Fig. 1. Regions of dynamical behaviors
for Eq. (1) for various values of the time delay.

Fig. 2. Attractors for the system
in Eq. (1) with
a = 1.6 and
b = 0.1 for various values of the
time delay.
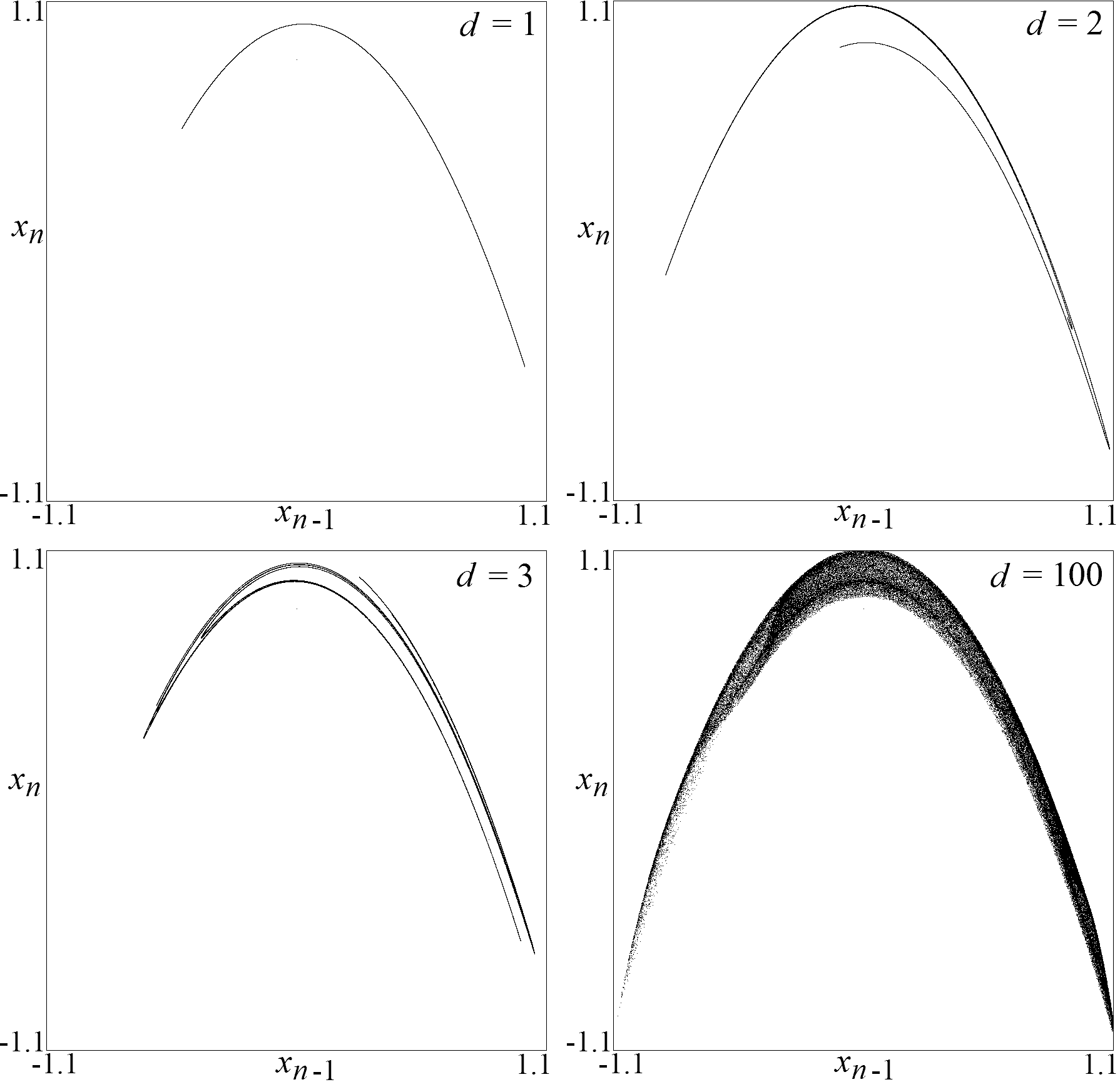
Fig. 4. Kaplan-Yorke dimension and
Lyapunov exponents for the system in Eq. (1) with
b = 0.1 showing the route to chaos
at low dimension (
d = 2) and
high dimension (
d = 100).

Fig. 5. Kaplan-Yorke dimension
and a few of the largest Lyapunov exponents for the system in Eq. (1)
with
b = 0.1 and
d = 100 showing in more detail the
onset of chaos.
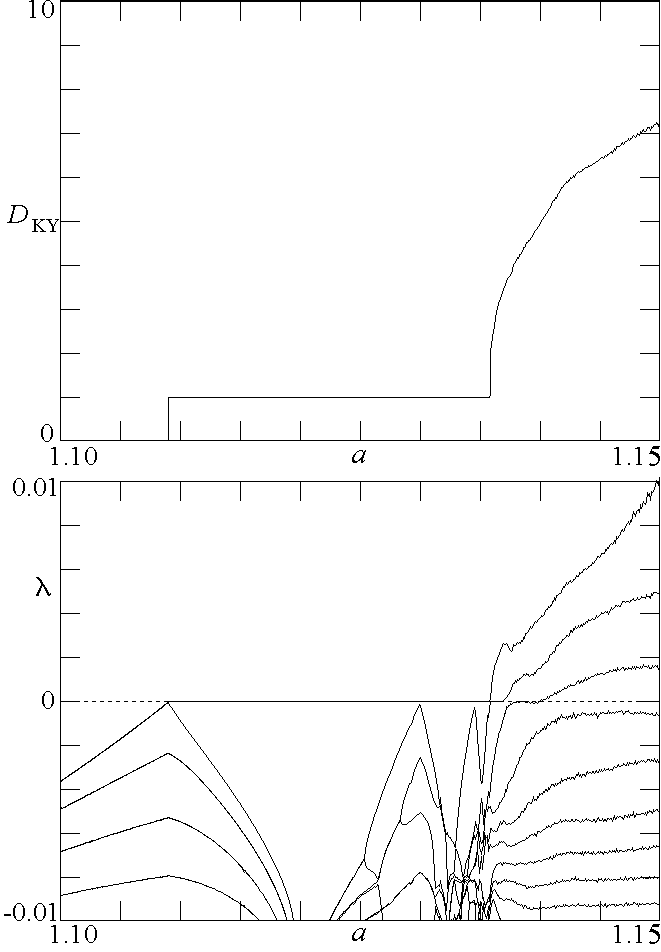
Fig. 6. Attractors for the system
in Eq. (1) with
b = 0.1 and
d = 100 showing period doubling of
a drift ring approaching the onset of chaos.

Fig. 7. Global bifurcations and
multiple attractors for two values of
b
with
d = 100.
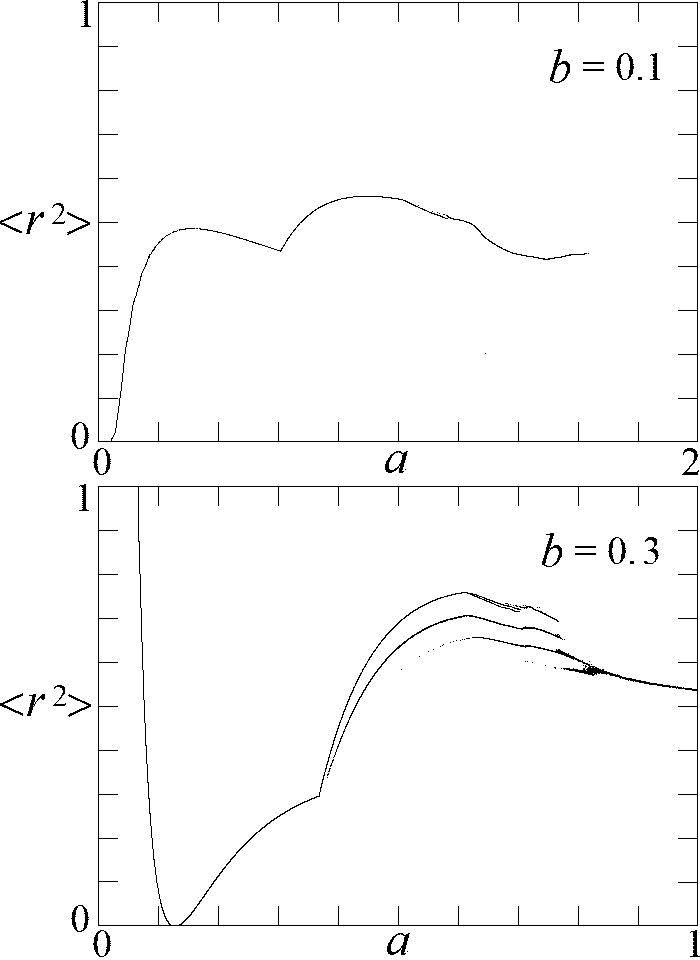
Fig. 8. Relative probability of
different values of <
r2>
for
a = 0.7,
b = 0.3, and
d = 100, indicating the existence
of at least seven distinct attractors.

Fig. 9. Four coexisting
attractors for
a = 0.7,
b = 0.3, and
d = 100 near the onset of chaos.