
Perhaps the algebraically simplest examples of sinusoidally-driven conservative chaotic flows are of the form:
d2x/dt2 + f(x) = A sin wt
A variant of simulated annealing was used to find the value of w
that maximizxes the Lyapunov exponent (base-e) for A
= 1 for various f(x) with the following results:
| Equation | Lyapunov
exponent |
| d2x/dt2 + sin x = sin 0.50t | 0.163 |
| d2x/dt2 + x3 = sin 1.88t | 0.097 |
| d2x/dt2 + x5 = sin 2.19t | 0.163 |
| d2x/dt2 + x7 = sin 2.32t | 0.198 |
| d2x/dt2 + x9 = sin 2.58t | 0.230 |
| d2x/dt2 + x11 = sin 2.79t | 0.242 |
| d2x/dt2 + x3 - x = sin 1.87t | 0.164 |
| d2x/dt2 + x|x|-1/2 = sin 5.57t | 0.123 |
| d2x/dt2 + x|x| = sin 1.61t | 0.051 |
| d2x/dt2 + x|x|3 = sin 2.00t | 0.139 |
| d2x/dt2 + sinh x = sin 1.54t | 0.014 |
| d2x/dt2 + tanh x = sin 0.27t | 0.009 |
All cases had initial conditions of dx/dt = x = 0.
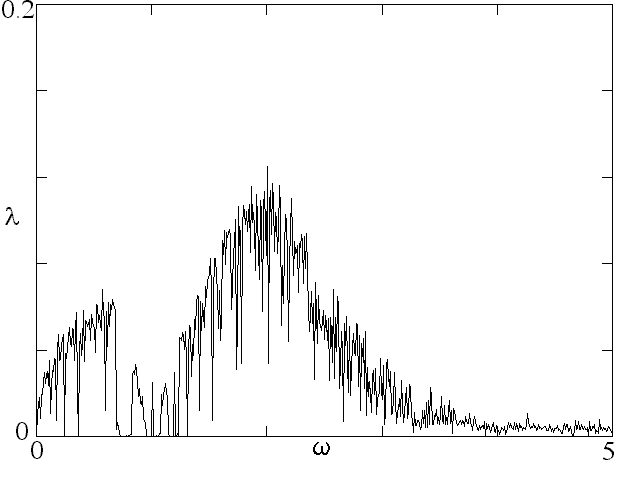
Hans Gottlieb (private communication, 14 Dec 2000) has pointed out that the case with f(x) = x3 is especially interesting because it may be the simplest sinusoidally-driven chaotic system. It is the dissipationless limit of the Ueda oscillator. It has a single parameter w. The plot below shows how the Lyapunov exponent for this system varies with w:

A Poincare section in the x-dx/dt plane for wt mod 2pi = 0 is shown below:

More generally, the system
d2x/dt2 + x|x|p-1 = sin wt
has chaotic solutions for a range of p and w. For example, the case p = 5 appears as follows:

The Lyapunov exponent for arbitrary p and w is shown in a gray scale below for initial conditions dx/dt = x = 0:

Chaos also occurs in nonlinear oscillators driven with square waves rather than sine waves. For example the system
d2x/dt2 + x3 = sgn(sin wt)
exhibits chaos over a wide range of w as shown below:
This system has the virtue that it may be possible to find an analytic solution.
Ref: J. C. Sprott, Chaos and Time-Series Analysis (Oxford University Press, 2003), pp.192-193.