Elementary quadratic chaotic flows with no equilibria
Sajad Jafari
a,∗, J.C. Sprott
b, S. Mohammad
Reza Hashemi Golpayegani
a
aBiomedical Engineering Department, Amirkabir
University of Technology, Tehran 15875-4413, Iran
bDepartment of Physics, University of
Wisconsin, Madison, WI 53706, USA
Received 23 October 2012
Received in revised form 5 January 2013
Accepted 7 January 2013
Available online 16 January 2013
Communicated by C.R. Doering
Three methods are used to produce a catalog of
seventeen elementary three-dimensional chaotic flows with
quadratic nonlinearities that have the unusual feature of
lacking any equilibrium points. It is likely that most if not
all the elementary examples of such systems have now been
identified.
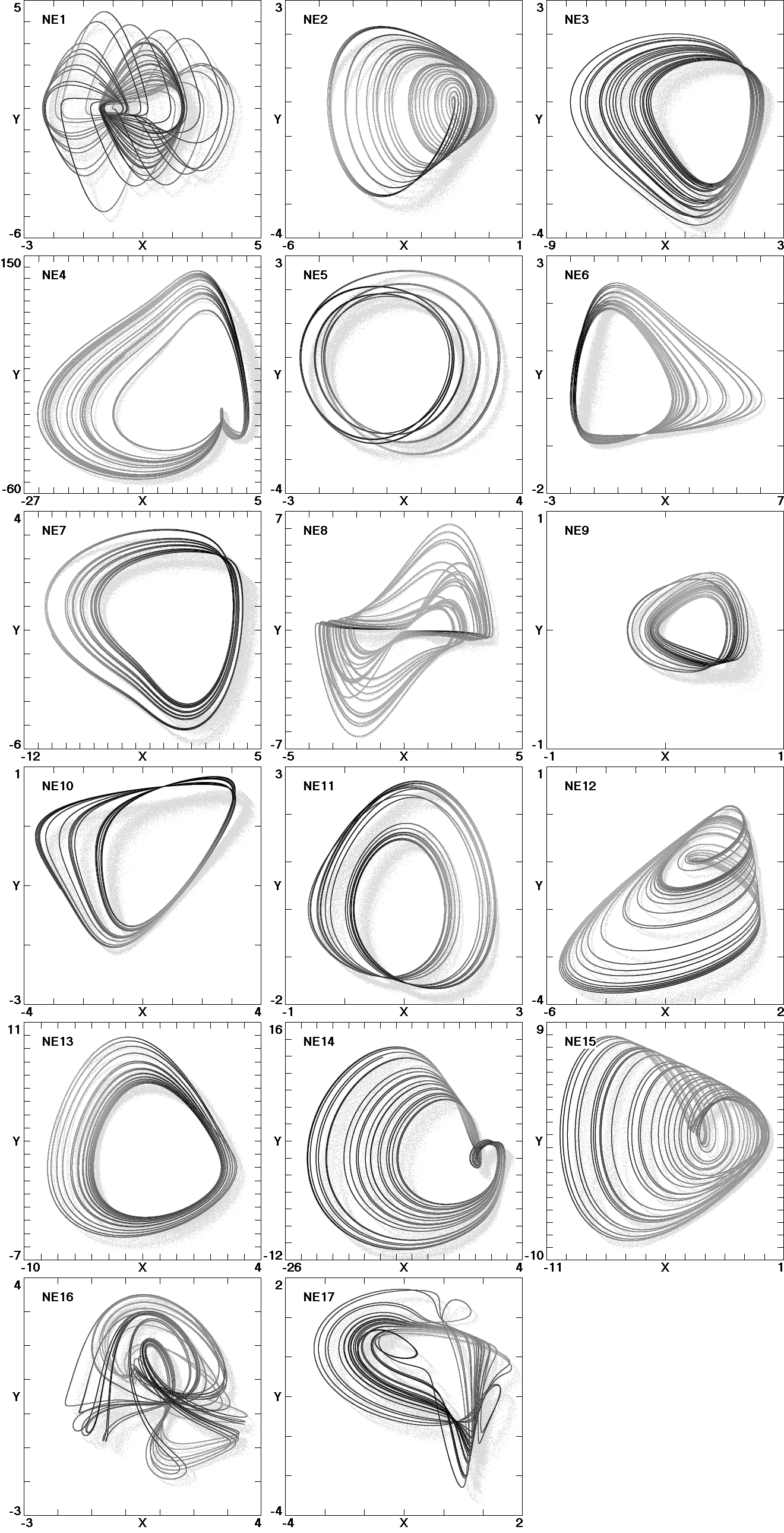
Fig. 2. The largest Lyapunov exponent and bifurcation diagram of
NE
6 showing a period-doubling route to chaos.


